ネットワーク科学 人間や物の関係性をデータから解明する学際領域

今日では、ネットワークは、インターネットから社会的ネットワーク、そして生物学的存在を決定づける遺伝的ネットワークに至るまで、あらゆるところに存在している。ソーシャルネットワークの形式化を唯一かつ明確な目的とし ている企業は、20億人を超えるアクティブユーザーを抱えている。これらの企業は社会科学の理論に触発されて、集中的に計画された巨大 なソーシャルエンジニアリングを行っている。

これらの企業はもちろん、文明化された世界全体で日常生活に欠かせないものとなっているインターネットに依存している。電話、電力、道路などの地味で、時には古代のインフラでさえも、今では当然ネットワークと呼ばれている。ネットワークという概念は、中央集権的なヒエラルキーでもなく、完全に非構造化されているわけでもない組織の一形態として、信じられないほど広く普及している。

ネットワーク科学とは

ネットワーク科学は、新しい学問分野を統合し、発展させることを目的とした学際的な領域である。物理学からコンピュータ科学、工学、経済学、社会科学まで幅広い知見を基盤に発展してきた経緯がある。この学問が対象とする分野はとても広く、「6次の隔たり」の起源から、ネットワークがなぜランダムな障害に強いのかの説明、エボラやH1N1のようなウイルスがどのようにして広まるのか、また、私たちの友人が私たちよりも多くの友人を持つのはなぜなのかまで、多種多様である。

1998年、コーネル大学の2人の物理学者ダンカン・ワッツとスティーブン・ストロガッツはネットワークの「スモールワールド」モデルを発表した。このモデルは、私たちが慣れ親しんできた規則的な格子状のネットワーク構造からのエキゾチックな逸脱に過ぎないと思われていましたが、彼らの考え方に同調する論文が出版されればされるほど、このモデルは研究者たちの間では「スモールワールドモデル」と呼ばれるようになった。

しかし、この論文が様々な分野の科学者に受け入れられていくうちに、この論文が、伝染過程から情報拡散に至るまでの実世界の現象における動的な振る舞いや相転移の理解に深い意味を持つことが明らかになった。この論文が、ネットワーク科学を学際的な分野として確立するための研究の新時代を切り開いたことは、すぐに自明のこととなった。

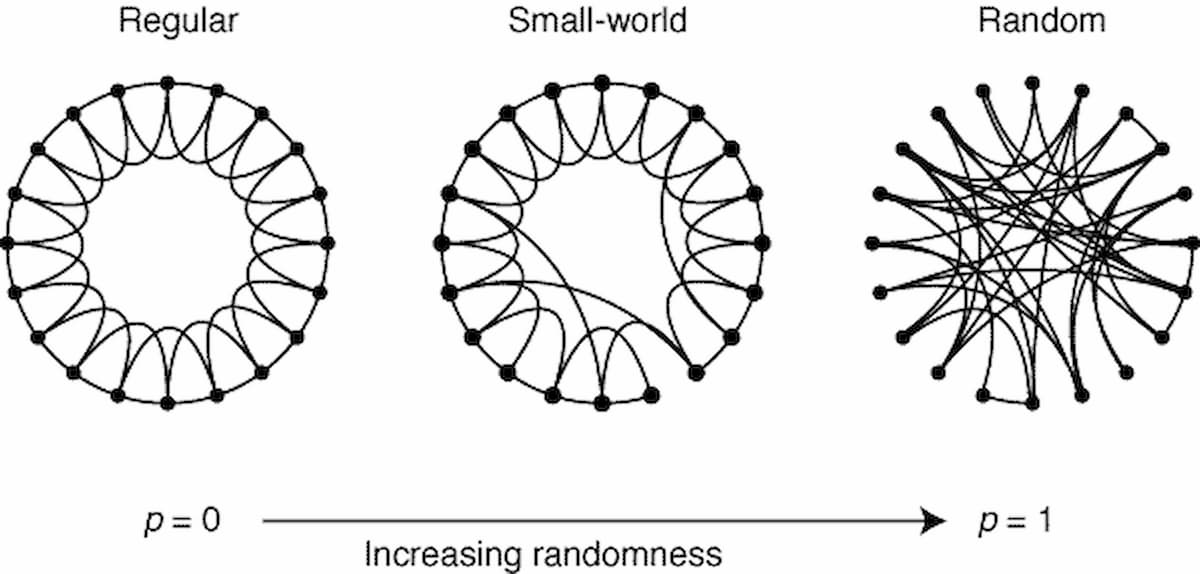
ワッツとストロガッツが論文を発表するまでは、典型的なネットワーク生成アルゴリズムは、1959年に発表されたErdös-Rényiモデルで記述されたような構築プロセスに基づいていた。これらのプロセスは、ネットワークにおけるノード間の接続（エッジ）の生成を導く原理を知らないことを特徴とし、与えられた接続確率でランダムにノードのペアが接続できるという単純な仮定をしている。ワッツとストロガッツの発見は40年ぶりの知の進歩だった。

ワッツとストロガッツのモデルは、当初は単に「6次の隔たり」を説明するものと考えられていた。しかし、このモデルが最も重要な影響を与えたのは、ネットワーク構造がさまざまな動的現象に与える影響の研究への道を開いたことかもしれません。1999年には、バラバシとあルベルトが「優先的選択」ネットワークモデルを提案し、実世界のネットワークにおけるノード間の接続数を記述する確率分布が、ランダムネットワークで予測されるポアソン分布ではなく、しばしば「ヘビーテール」分布（べき分布）によって特徴づけられることを強調した論文を公開しました。クラスター化された接続性（WattsとStrogatzのモデルのような）と不均一な接続性（優先的接続モデルのような）を持つネットワークに内包されている創発的な行動と相転移の広範なスペクトルは、多くの分野の科学者の注目を集めた。いわゆる「スケールフリー・ネットワーク」の提案である。

その後、一連の発見が続き、そのようなネットワークの複雑な構造が、ネットワークの堅牢性、伝染病の蔓延、情報の流れ、ネットワークをまたぐ集団行動の同期化のための意味合いを持って、実世界のシステムを支える方法を説明している。例えば、スモールワールドの接続性パターンは、World Wide Webの構造や、脳の解剖学的・機能的領域がどのように相互に通信しているかを理解するための鍵となることが証明されている。モジュール性や構造モチーフの概念など、ネットワークの他の構造的特性が、その後すぐに顕微鏡下で観察されるようになった。

現在のネットワーク研究の世代は、前例のない計算能力、ビッグデータセット、新しい計算モデリング技術の恩恵を受ける分野を相互に融合させ、個々のノードのダイナミクスとマクロなネットワークの創発的な特性の間の架け橋となっています。しかし、スモールワールドモデルや優先的付着モデルの即時性とシンプルさは、今でもネットワークトポロジーの理解を支えている。実際、これらのモデルがさまざまな科学分野に関連していることが、現在ネットワーク科学として知られている学際的な分野の基礎を築く主要因だった。Axionでしばしば登場する計算社会科学もまたこのネットワーク科学から派生した類型の1つである（関連記事：計算社会科学とは コンピュータ科学と社会科学の婚姻）。

ネットワーク、クラウド、市場

ネットワーク科学をコンピュータ科学やデジタル経済の文脈に取り入れて理解するときに有用なのが、コーネル大学経済学部教授のデイビッド・イーズリーとコーネル大学情報学科教授のジョン・クラインバーグによる『Networks, Crowds, and Markets』（リンク）である。本書は、半自律的でありながら相互依存的な単位からなるネットワークと、それらのネットワークが個人の行動や小規模な相互作用から生じる大規模なパターンをどのように形成しているかを研究する「ネットワーク科学」と呼ばれるものについての教科書の一つである。

ネットワーク科学では、基本的に、ネットワークはノード、つまり頂点からなるグラフとして表現され、その一部は「エッジ」と呼ばれるリンクで結ばれている。これらのエッジは方向性や強弱などの属性を持っていてもいなくてもよいのですが、基本的な前提として、個々のノード間の重要な関係は二項関係、つまり二項関係から構築できる関係であるということが挙げられる。グラフ理論は、ネットワークについて推論するための数学的ツールのセットを提供し、それらについての理論を明確にするためのものだ。

本書は、ゲーム理論家が「合理性」と呼ぶ考え方をエージェントの行動に対し適応することで、様々な想定の確実性を担保している。同書が言及する進化論的ゲーム理論では、戦略を選択する前向きで計算高いエージェントに焦点を当てるのではなく、エージェントが後ろ向きで適応的な方法で採用する戦略そのものに焦点を当てる。つまり、過去に他の人にとってうまくいっていたと思われることをより多く行い、うまくいかなかったことをより少なくするのである。古典的なゲーム理論が想定する文字通りの超人的な計算能力とは大いに異なるものだ。だから進化論的ゲーム理論は、模倣によって学ぶことができる唯一のエージェントを必要とし、イーズリーらは現実主義への実質的なステップを構成している。

本書は、他にも、ネットワークの構造と戦略的相互作用を、オークション、マッチング市場、仲介者のネットワークとの取引、ネットワーク上の交渉ゲームなど経済学の領域で、いくつかの設定を検証している。

情報ネットワークとワールド・ワイド・ウェブは計算社会科学の前提であり、最重要の探索領域である。本書は、Googleを構成する「ページランク」という方法と、「ハブとオーソリティ」を使ったリンク分析というクラインバーグのライバルシステムにふれている。大雑把に言えば、ウェブページのページランクは、それ自体が高ランクのページからのリンクをどれだけ持っているかを反映している。

この場合は、いわば、ウェブグラフ上のランダムな歩行の軌跡に関連して、固有の定点に縮小することができる。ハブとオーソリティシステムも似ていますが、オーソリティとして、あるいはハブとしての質に基づいてページを区別する。このアプローチは、多くの点でページランクよりも数学的にも概念的にもエレガントであり、なぜこのアプローチが流行らなかったのかは、明らかではないかもしれない。

不確実な情報に直面した人々が、他の人の行動や行動を手掛かりにして、自分自身が何をすべきかを判断し、それによって、おそらく非常に小さな、あるいはまったくランダムな、あるいは誤解を招くようなシグナルを増幅させ、多数の人々が順次同じ決定を行う減少がある。これを「情報のカスケード」（Information cascade） と呼ぶ。

参照文献

1. Duncan J. Watts, Steven H. Strogatz. Collective dynamics of ‘small-world’ networks. Nature volume 393, pages440–442(1998).
2. Barabási, A.-L. & Albert, R. Emergence of Scaling in Random Networks. Science 286, 509–512 (1999).
3. David Easley, Jon Kleinberg. Networks, Crowds, and Markets: Reasoning about a Highly Connected World. Cambridge University Press, 2010.

Photo by Ratapan Anantawat on Unsplash