DeepMind、電子の挙動をシミュレートする FermiNet をオープンソース化

9月、Alphabet社傘下のDeepMind社は、量子化学計算において、波動関数の近似をニューラルネットで行うFermi Netについて詳しく説明した論文をPhysical Review Research誌に発表した。DeepMind社が提案するFermiNetは、原子エネルギーを計算するためのAIの最初のデモンストレーションの1つであり、現在GitHubでオープンソースとして公開されている。

シュレーディンガー方程式は約100年前から知られていた。しかし、この方程式は、水素原子よりも複雑なものについては、閉じた形で解くことは不可能だ。コンピュータがあるのとほぼ同じくらい長い間、人々はこれらの計算式を解いてきたが、化学に関連するこれらの計算には信じられないほど高い精度が必要とされる。そこで、実行可能な計算量になるように近似を行うが、近時の程度と計算精度がトレードオフとなる。

このトレードオフを克服するには、物理法則からの要請を満たし、効率的に計算可能な波動関数の表現方法が求められる。計算科学の従来手法には、反対称性を満たす波動関数としてのスレーター行列式を利用するものがあった。

DeepMindの研究チームは、物質の大部分を構成する粒子であるフェルミオン系の波動関数を表現できる新しいニューラルネットワークアーキテクチャを開発し、従来の近似波動関数よりもはるかに正確であることを示した。

既存の計算量子力学ツールには幅があるが、効率的な表現の問題に対処するためには新しい方法が必要だと研究チームは考えた。分子動力学のような古典的な化学計算手法では数百万個の原子を扱うことができるのに対し、最大規模の量子化学計算では、最も近似的な手法でも数万個の電子しか扱えないのには理由がある。古典的なシステムの状態は簡単に記述できる。しかし、量子系の状態を表現するのは、はるかに困難だ。電子の位置のすべての可能な構成に確率を割り当てなければならない。これは波動関数にコード化されており、電子の配置ごとに正または負の数を割り当て、波動関数の2乗はその配置でシステムが見つかる確率を与えます。もしそれを各次元に沿って100個の点を持つ格子として表現しようとすると、シリコン原子の電子配置の可能性の数は宇宙の原子の数よりも大きくなる。

研究チームは、ディープ・ニューラル・ネットワークが助けになると考えた。ここ数年、複雑で高次元の確率分布をニューラルネットワークで表現することに大きな進歩があった。彼らは、これらのネットワークが人工知能の問題で高次元関数に適合することがすでに証明されていることを考えると、量子波動関数の表現にも使えるのではないかと推測した。

ジュゼッペ・カルレオ（ローザンヌ大学助教授）やマティアス・トロイヤー（マイクロソフトリサーチ・ディスティングイッシュトサイエンティスト）などの研究者は、現代のディープラーニングが理想化された量子問題を解くためにどのように利用できるかを示してきた。DeepMindの研究チームは、ディープニューラルネットワークを使って化学や凝縮系物理学のより現実的な問題に取り組みたいと考えていたが、それは計算に電子を含めることを意味していた。

電子を扱う際には一つだけ課題がある。電子はパウリ排除の原理に従わなければならない。これは、電子がフェルミオンと呼ばれる粒子の一種で、陽子、中性子、クォーク、ニュートリノなど、ほとんどの物質の構成要素を含んでいるからだ。電子の波動関数は反対称でなければならない。2つの電子の位置を入れ替えると、波動関数は-1倍になります。つまり、2つの電子がお互いの上にある場合、波動関数（とその配置の確率）はゼロになるということだ。

このため、入力に対して反対称性を持つ新しいタイプのニューラルネットワークを開発しなければならなかった。ほとんどの量子化学の手法では、反対称性は行列式と呼ばれる関数を用いて導入される。行列の行列式は、2つの行を入れ替えると、フェルミオンの波動関数のように出力に-1が乗算されるという性質を持っている。つまり、関数の束を取り出し、系内のすべての電子について評価し、その結果を1つの行列にまとめることができる。その行列の行列式は、適切に反対称性のある波動関数となる。この方法の大きな制限は、結果として得られる関数（スレーター行列式として知られている）があまり一般的ではない。

波動関数は、通常、はるかに複雑だ。これを改善するための典型的な方法は、スレーター行列式の大規模な線形の組み合わせ（時には数百万以上）を取り、電子の対に基づいていくつかの単純な補正を加えることだ。その場合でも、これだけでは正確なエネルギーを計算するのに十分ではないかもしれない。

提案手法であるFermiNetでは、行列式に入る各関数を全電子の関数にすることでこれを実現している、と論文は主張する。これは、単に一電子と二電子の関数を使う方法をはるかに超えている。FermiNetでは、各電子に対して別々の情報の流れを持っている。これらの流れの間に相互作用がなければ、ネットワークは従来のスレーター決定論よりも表現力はない。これを超えるために、ネットワークの各層のすべてのストリームからの情報を平均化し、この情報を次の層の各ストリームに渡す。このようにして、これらのストリームは、反対称関数を作成するための正しい対称性の特性を持っている。これは、グラフニューラルネットワークが各層で情報を集約する方法に似ている。スレーター行列式とは異なり、フェルミネットは、少なくともニューラルネットワークの層が十分に広くなる限界においては、普遍的な関数近似器である。つまり、これらのネットワークを正しく訓練すれば、シュレーディンガー方程式のほぼ正確な解を得ることができるはずだ、とDeep MindのリサーチサイエンティストのDavid Pfauは論文の中で主張した。

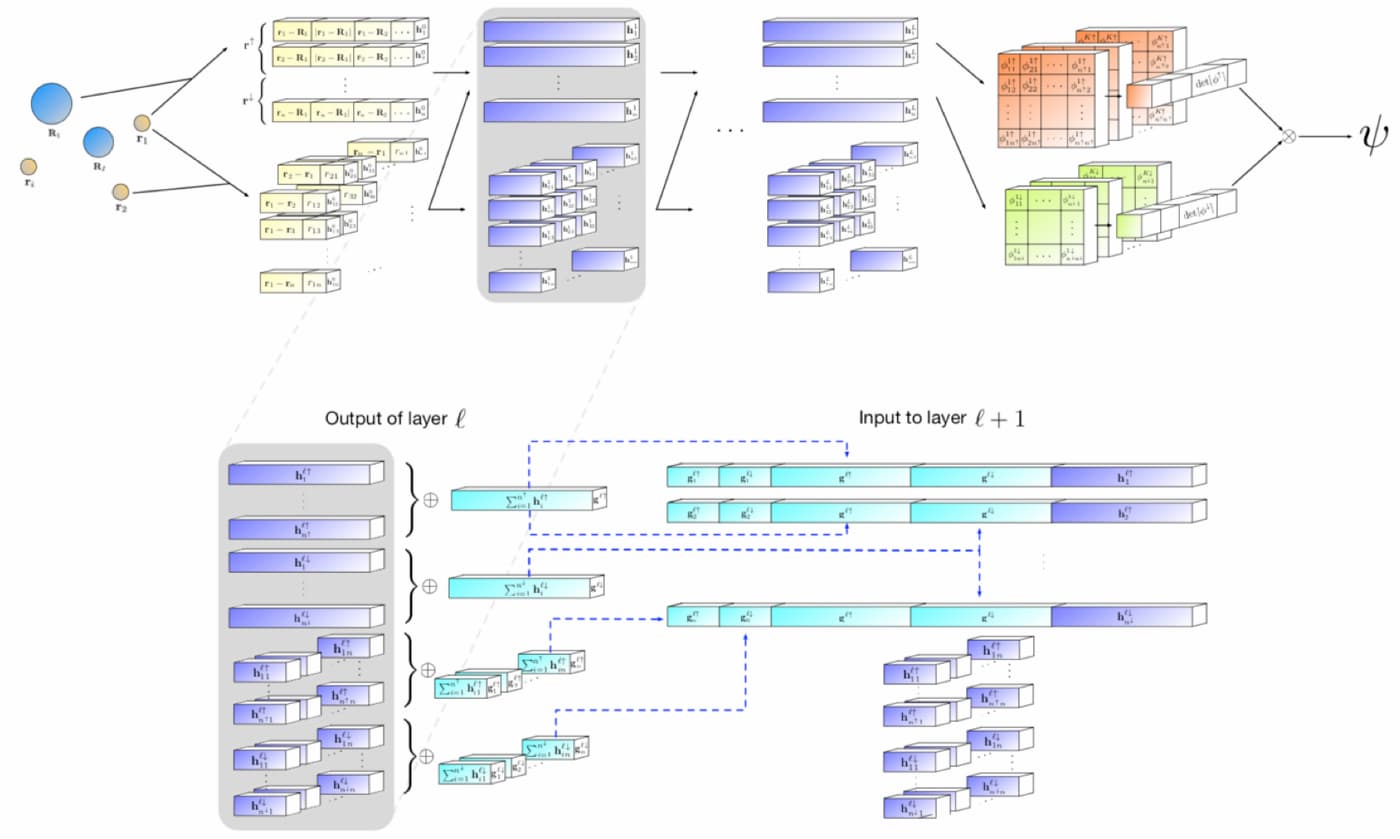
「FermiNetは、第一原理から原子や分子のエネルギーを計算するための深層学習の最初の実証であり、有用なほど正確であり、現在でも最も正確なニューラルネットワーク手法となっている」とPfauらは記述している。「DeepMindでのAI研究で開発されたツールやアイデアが、自然科学の根本的な問題の解決に役立つことを願っており、FermiNetは、タンパク質の折りたたみ、グラッシーダイナミクス、格子量子色力学、その他多くのプロジェクトでの研究に加わり、そのビジョンを実現している」と述べている。

参考文献

1. David Pfau, James S. Spencer, Alexander G. D. G. Matthews, and W. M. C. Foulkes. Ab initio solution of the many-electron Schrödinger equation with deep neural networks. Phys. Rev. Research 2, 033429 – Published 16 September 2020.